Jamming Jack Studs

The nice thing about a stiff beam is that it won’t sag much. The not-so-nice thing is that it won’t `give’.

In new construction, wood framing more or less starts from the ground up; wood members are placed on top of one another, and are fastened into place. Just about everything is `statically determinate’, and unless something is cut grossly wrong, things `fit into place’. In remodeling, on the other hand, walls, etc. are removed, surrounding or supporting framing is more or less supported (`shored’), and new construction (beams, etc.) put (sometimes `jammed’) into place. Even with the best intentions, things don’t always `fit’. And when they don’t fit, the common remedy is the hammer, big or small. A common situation is removing a wall placing a header or beam over the new space; the header supporting the framing above, floor or roof/ceiling. While the header (or beam) can be ordered and cut to easily fit, it’s the supports at the ends of the new opening, typically studs (jack studs), that often don’t quite fit.

So let’s look at a recent wall-removed-header-placed `situation’. Roof and ceiling framing were shored using temporary walls on both sides of the existing wall, adjacent to planned opening. The wall framing, from sole plate up to but excluding the double top plate, was removed, and the new header `lifted’ into place (human labor). Some of the jack studs, intended to support the ends of the headers, cut beforehand, didn’t quite fit. Alas the hammer. After a lot of smashing, the jack studs were in place, supporting the header, readying for the removal of the temporary walls. Not quite!

Let’s run some numbers.

The header was designed to have very little `sag’ … `deflection’ in engineer language (as well, of course, be strong enough). The existing wall held up ceiling and roof framing above; the new header would take over the role of the wall above the new opening. The clear span for the header is 10’-9”. Two jack studs were used for support each end. In the design headers, beams, etc., the `structural’ span for the header is taken to extend half way into each support, so, 10’-9” + 2 x ½ of 2 x 1.5” = 10’-9” + 3” = 11.0 ft. The header is a 2-ply 1.75-in. x 11.875-in. 2.1E LVL. The `design’ of the header accommodated the design load by several hundred percent, with, importantly, very little anticipated deflection, or `sag’ (very stiff header). The intent was that the top of the opening be visually `flat’.

The jack stud rammed into place at one end caused the header to be `bent’, with respect to a straight line end to end, about 1/16th of an inch. (Lots of ramming). This `bent-ness’ was before the shoring was removed. Properly shored, and assuming a flat (straight) ceiling/roof above, the header initially should `fit’ under the framing with no deflection; it’s not carrying any load! Only as shoring is removed should the header take on load, and begin to bend. Structurally, the action of forcing the header to be bent into a curved shape, however `slight’, produces, in the wood, the same effect as if the header was simply supported at ends (just `resting’ on supports), and being loaded downward along the span, enough to bend it. The load comes about as jamming the jack stud(s) in place tends to `lift’ the header and framing on top of it … the framing above resisting the lifting action, pushing down.

Assuming this `lifting’ effect is greatest at the end where the stud is jammed in place, and tapers off to … nothing, or little, at the other end, we’ll model the situation using the so-called `SIMPLE BEAM-LOAD INCREASING UNIFORMLY TO ONE END’, found in typical engineering design manuals. (See graphic.) Let’s look at the load `required’ to produce a 0.10-inch deflection.

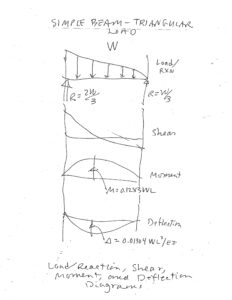
Δ = 0.01304 W L^3 / EI,

where,

Δ = deflection (sag, out-of-straightness),

W = the `whole’ load (`weight’) or downward force on the beam (header),

L = header span, 11 ft or 132 in.

E = the modulus of elasticity of the header, 2,100,000 psi (the `2.1E’), and

I = area header moment of inertia of the header , n x (b h^3/12) = 1.75 (11.875)^3 / 12,

where

n = number of plies,

b = thickness of each ply, and

d = depth of the header.

We get, for I, 488 in.4.

Solving for W, we get, … W = 2,137 lb (call it 2,100 lb).

Hmmmm. The total dead load (roof and ceiling weight) above the header is about 2,300 lb, and more or less distributed uniformly. By smashing the jack stud in place we are just about starting to `lift’ the roof. No. Take the jack stud(s) out, take off a sixteenth of an inch or so, so that it goes in with less `smashing’.

Can’t we just leave the header as is, since it, and the jack studs, are in place, and nothing `happened’? After all, the header was intended to carry the roof weight anyway!

Maybe, but why? What if the out-of-straightness is 1/10th of an inch? … or 1/8th of an inch? At 1/8th of an inch we’d be well overcoming the weight of the roof … things would start to `give’ that we don’t want to give. Additional to the noise from the banging of jack studs in place, we might be able to hear creaking and groaning as the framing (wood members and fasteners and other materials) above and adjacent to the header start crushing, yielding, cracking. At some point we could, theoretically, `break’ the header itself (if we haven’t already broken something else … maybe the jack stud). Besides, we’d be carrying the roof wrong … by the end of the header, not equally along the entire span.

Are you SURE nothing happened? Is the roof plane still straight? Have you cracked any gypsum?

The header is now pre-bent, and pre-loaded. Is the out-of-straightness visible? So far the header is only carrying the weight of the roof itself, plus some more. What happens when the header experiences its `design load’ (a future re-roofing project)? In this particular case, re-running the design calculations with some extra load (and deflection) might turn out to be `okay’ (as there was way more strength, and stiffness in the header than required), but, again, why? Take the studs out and do it right. The header should rest snug, tight, on top of the studs, but not so jammed as to deflect the beam.

…

Where a header or beam is more deeply embedded in a structure, and, particularly, if the structure has continuous framing elements or inflexible systems, providing little `give’, it’s possible, by `jamming’ studs into place, to induce a load in the header that exceeds the design load. Not good.

Don’t ruthlessly smash studs or columns into place; cut them so they fit. Tight, yes! And with a bit of pounding; but you don’t want the header ends to `settle’ (move) when the shoring is removed.

…

A NOTE ON NUMBERS

The numbers in the calculations above look rather `exact’. Actually, many are not. For example, the modulus of elasticity value, E, for the header is (published) 2.1E, meaning 2,100,000 psi. This is an average value. A bunch of LVL specimens were measured in a test lab for E, and the average value was used (published). Some of the LVLs that arrive on a project (or lumber yard) have higher E, some lesser. That’s the way wood is, variations in properties, between species, between grades in species, and between `engineered lumber’ (e.g., LVL) made up of wood. (LVL tends to have less `variation’ than other wood products, due to how it is manufactured … that is another conversation.) So, when I dump and un-exact number E into an equation that looks exact (and, in fact, might very well be), I get an un-exact number out. The applied force to bend an 11-foot long 2-ply 1.75 x 11.875 2.1E LVL header 1/16th of an inch may take somewhat more, or somewhat less, than the one I calculated; in fact, it would be highly unlikely that it would take, exactly, 2,137 lb to bend the header 1/16th inch, exactly.

Further, the deflection equation used does not account for `shear deflection’. Shear deflection is the relatively small amount of additional `sag’ that a beam, header, joist, girder, whatever, experiences due to the `shearing’ of the wood fibers. The equation used above only determines the deflection (sag) that comes about from bending stresses (compressing the top of the beam and elongating the bottom). By neglecting the shear-deflection term I have been a bit `conservative’ – a lesser amount of force (jamming) could indeed produce the same effect. (The header is a tiny bit less stiff than I calculated.) But, this `shear deflection’ may very well be (more than) eclipsed by the variation in E, already discussed above (and talked about more in some of my other posts).

Don’t worry so much about the exactness in E; worry about cutting the studs so that they don’t need to be ruthlessly smashed into place.

…