Wind Forces on a House (Compared to a `Shop’) – ASCE 7-22 – MWFRS – Envelope Procedure

In previous examples (here and here) we looked at the horizontal and vertical wind forces on a `shop’. The shop is/was a `pretend’ structure in a real location, Latah County, Idaho. It derives from an actual shop of the same dimensions, but in a very different location. The intended use in the example was, as with the real one, `uninhabited’ occasional (hobby) farm use. As such, we assigned in a Risk Category of I, per Chapters 1 and 26 of ASCE 7-22.

Here’s a summary of relevant information from the shop example:

Basic Wind Speed: 96.5 miles per hour (mph)

Exposure C

Kd = 0.85

Kzt = 1.00

Ke = 0.915 (Elevation 2500 ft)

Roof Slope: 18.4°

Mean Roof Height: 12.3 ft (0.5 ft stemwall + 8.5 ft framed wall + ½ of the roof height of 6.67 ft)

Kz, Kh = 0.85 (Table 26.10-1, from the Exposure Condition and Mean Roof Height)

(Total Roof Height: 15.7 ft, in case we want it later)

We found with that example that the design horizontal and vertical wind forces, for an 8-foot wide transverse `swath’ of building not near the ends, were 1,000 lb and 5300 lb, respectively. The vertical (uplift) wind force on the shop (swath) is over 5 times than that of the horizontal force. The shop wants to act like an airfoil and `fly’ away in the design wind.

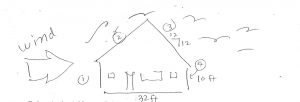
Consider another pretend structure, a `house’, near the shop (also located in Latah County, Idaho). The house width is 30 feet (ft), one story, with 9-ft framed walls on 12-in. (deep) framed floor system on 6-inch stemwalls, and with roof pitch of 12/12. (Note the steepness of the roof … 45° slope.) The total height of the house is 0.5 ft + 1 ft + 9 ft + ½ of 32 ft x 12/12, or 26.5 ft; it is significantly taller `than’ the shop. Let’s calculate the total horizontal and vertical design wind forces on the house.

To determine the wind forces on the house we will, as with the shop, use ASCE 7-22 Chapters 26 General Requirements, and Chapter 28, Envelope Procedure. The steps are given in Table 28.2-1. Here goes:

Step 1: Determine the Risk Category: easy; it’s Risk Category II (ASCE 7-22 Table 1.5-1).

Step 2: Determine the Basic wind speed, V. Here’s where it gets a bit interesting. Even though the house is potentially `right next to’ the shop, we end up using a different wind speed. Why? It’s because we are assigning different `risk’ to house, versus shop. We’re willing to risk an 86.5-mph wind hitting the shop, and possibly `blowing it over’, but we’re not willing to risk that same wind blowing over the house. That’s how the `code’ parses it. For the sake of example, we could determine the wind forces on the shop based on Risk Category II, as, say, for business use or, at least, regular use by persons. In fact, the real shop, upon which the examples derive, was at times used for a business. However, in that case, I would assume that, for the wind event, the big garage doors would be closed; then I would have smaller internal pressure coefficients, and lesser total wind uplift forces. I’ll stick with Risk `Categ’ I and open garage door (partially enclosed structure).

Basic wind speed, for the house, Risk Category II, ASCE 7-22, Figure 26.5-1B, 102.5 mph.

Step 3: Determine the wind load parameters:

Wind directionality factor … same as for the shop; Kd = 0.85.

Exposure Category … same as for the shop; C.

Topographic factor … same, Kzt = 1.0.

Ground elevation factor … same, Ke = 0.915 (2500 ft elevation).

Enclosure classification: Section 26:12; `Enclosed’.

Internal pressure coefficient, GCpi, from Section 26.13 / Table 26.13l-1; GCpi = +/- 0.18.

Step 4: Determine the velocity pressure exposure coefficient, Kz or Kh, from Table 26.10-1. First we need the mean roof height; it is, 0.5 ft + 1.0 ft + 9 ft + ½ of 32 ft x 12/12 x ½ = 18.5 ft. From Table 26.10-1 I get Kz, Kh = 0.885 (interpolated).

Step 5: Determine the velocity pressure, qz or qh, using Equation 26.10-1. Here goes:

qz = 0.00256 Kz Kzt KeV² = 0.00256 (0.885)(1.0)(0.915)(102.5²) = 21.8 psf.

(Recall for the shop we had qz = 18.5 psf.)

Depending on the actual pressure coefficients, this higher qz may, or may not, result in higher pressures on wall and roof surfaces; let’s see.

Step 6: Determine the external pressure coefficients, GCpf. For our house we will, for comparison with the shop. again look at … the windward wall (Zone 1), windward roof (Zone 2), leeward roof (Zone 3), and leeward wall (Zone 4), Case 1, not near the end of the building. From Figure 28.3-1 we get the following external pressure coefficients (Load Case 1) … (45° roof slope) …

GCpf windward wall (Zone 1) = 0.56

GCpf windward roof (Zone 2) = + 0.21 (notice the `positive’)

GCpf leeward roof (Zone 3) = -0.43

GCpf leeward wall (Zone 4) = -0.37

We’ll look at positive internal pressures, for now, so GCpi = 0.18 (enclosed).

The resulting pressures are:

p, windward wall = qz Kd [(GCpf) – (GCpi)] = 21.8 psf (0.85) (0.56 – 0.18) = 7.0 psf

p, windward roof = 21.8 (0.85) (0.21 – 0.18) = 0.56 psf (external and internal pressures just about cancel)

p, leeward roof = 21.8 (0.85) (-0.43 – 0.18) = – 11.3 psf (negative meaning suction)

p, leeward wall = 21.8 (0.85) (-0.37 – 0.18) = – 10.2 psf (again, suction).

We’ll again consider an 8-ft `swath’ of building. And considering the `swath’ as a whole, the internal pressure coefficient (GCpi) acting on the inside faces of the (outside) walls cancel. (Yeah, the building is symmetric about its longitudinal axis.)

The wall areas are 8 ft wide x 10 ft tall = 80 sf.

The roof slope length (neglecting eaves) is … 16 ft √2 = 22.6 ft, each side, ridge to wall line.

The slope area, each side, for the 8-ft swath, 8 ft x 22.6 ft = 181 sf.

The wind forces are …

windward wall, F = p x A = 7.0 psf x 80 sf = 560 lb (horizontal)

windward roof, 0.56 psf x 181 sf = 101 lb (pushing in @ 45°)

leeward roof, 11.3 psf x 181 sf = 2045 lb ( … dropped the negative sign but understood to be sucking up and away)

leeward wall, 10.2 psf x 80 sf = 816 lb (suction).

Per the 45 degree roof slope, the horizontal and vertical forces are:

Fx = 563 lb + 101 lb (cos 45°) + 2045 (cos 45°) + 815 = 2900 lb (rounded a bit)

Fy = – 101 lb (sin 45°) + 2045 (sin 45°) = 1400 lb (rounded).

This is interesting. The horizontal wind load is greater than the vertical … and nearly twice so. Recall the vertical wind load on the shop was much greater than the horizontal wind load on the shop. The shop will tend to fly up and away in a big wind. This particular house would have a greater tendency to be pushed/pried off its foundation, and slide along the ground.

Provided neither started to get ripped apart first (Components and Cladding … stay tuned!).