weight of wood (posts)

Yesterday I went to the building supply store to get some pressure-treated 4 x 4 posts. (for more fence … gates, etc.!). I’m always amazed by how `wet’, and heavy, pressure-treated posts are, at the store. I pulled them from a fresh bundle, so perhaps they hadn’t been there long. And, yes, for 4 x 4’s, they seemed heavy, but I know better. Moist makes heavy! How heavy? Well, once home, I grabbed our bathroom scale, and a tape-measure, and weighed and measured them.

Here are the posts …

Here’s the data …

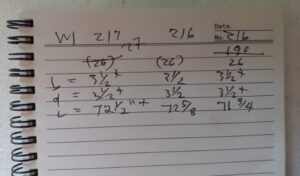
Here’s the calcs …

Whoa! … 50, 51 pcf!

The markings on the posts indicate they are `SYP’ (Southern Yellow Pine) No. 2. The `design’ weight for Southern Pine is 35 pcf, but this is for `dry’ service … essentially covered, conditioned structures. For lumber, `dry’ is defined as not exceeding 19 percent moisture content. (I’ll go check …) Depending on where I `poked’ the posts, I’m getting high 20’s, high 30’s, 40’s, and in some places pegging out at 50 (percent). There are `equations’ relating moisture content and the specific weight of wood; see, for example, the AITC Timber Construction Manual (Chapter 2), or the USDA Wood Handbook (Chapter depending on edition). We could play with the equation(s) provided therein, but what numbers would I plug in, as my moisture content readings are `all over the place’? The point here is: wet wood is heavy! And, if your wood is wet1, and you’re putting it to structural use, or it is supported by some structure, you must consider it’s heavier weight2. Pressure-treated wood is wet because it gets `dunked’, under pressure, to impregnate the, in this case, preservative treatment. It will dry out, some, in time, depending on where I end up using it.

This adventure in wood weight brings me back to what I have `always said’: “Here in America we learn engineering backwards.” We learn arithmetic in grade school, algebra and calculus in high school, in college more calculus, and then differential equations, and more numerical methods courses, and at some point start our engineering courses. The courses start with basic mechanics, then analysis, and by the time we graduate, one or several `design’ courses, all the while learning from textbooks.

Then we get a job, and we find out that in the real world, we design using codes and standards and `design manuals’. What about all those (expensive) textbooks? (I’m not suggesting you sell them, or even throw them away … somewhere down the line in your design journey, if one becomes useful for even a few minutes, it paid for itself, if you kept it.) As we trudge forward in our careers, it’s nice if we can see, up close, the materials we’re working with, and the structures we’re designing. Seeing failures is also instructive; hopefully not our own. And maybe we even build a few things ourselves, probably more out of hobby than necessity.

In my journey I have also actually `worked’ on construction crews. Not glamorous, but invaluable. I also worked as an engineer for a construction crew. Double invaluable. And now, even later in career, I am building more and more, primarily structures on our farm. Of late I have become more intimate with the weight of wood, especially the weight of wet wood, dealing with freshly sawn lumber, and pressure-treated lumber. When I was younger, it seemed the wood was always drier; plus, being younger, I was stronger; either way, I `didn’t notice’ as much.

So, in my opinion, an engineering education should be taught in reverse of the way it is now. First, while young and strong, the engineering `student’ should be required to get out there and build stuff … lift, carry, nail. Learn hands-on how much things weigh, what materials are used where, and why, which way things span, how far, and so on. Then enter the `classroom’. Enter the classroom with a real-world situation, with the assignment of coming up with a design, a safe design, a `buildable’ design … a bridge, a building, a … whatever. Be taught the theory, and then `why’ and `what’ captured by the corresponding `equations’. And if fancy math is needed, learn the fancy math. And, finally, the numbers should not be just ink on a page, or computer screen, but reflect reality.