dead load deflection
Jeff R. Filler, (c) 2021
The dead weight deflection of a beam, rafter, etc. is the amount the beam deflects, bends, sags, due to the `dead weight’ of the things it is carrying, including itself. Going back to the example of the rafters for my wife’s barn, we have 2 x 6 rough (actual dim) Southern Pine rafters spaced 24 inches on center, supporting 1 x 2 purling, and metal. So far I have supposed the whole assembly, rafters included, to weigh 5 pounds per square foot. Of course this is an average. Out there between the rafters is just the weight of the purlins and (thin) sheet meal roofing. And out there between the purlins is only the (thin) sheet metal. Out `there’ the weight of the roof is much less. But, if we add up the weight of the rafters, purlins, metal roofing, screws, and nails (yes, the Oxford comma), and smear it out over a per-square-foot basis, we’ll probably get (not more than) 5 psf.
Let’s look at the rafters.
They are 2 in. x 6 in., `actual’.
Now, Southern Pine (SP) lumber is `assigned’ a specific gravity of 0.55. This means that (on the average, of course, since wood is variable), (that) Southern Pine lumber weighs 55% times that of water, or 0.55 times 62.4 pounds per cubic foot (look it up if you want to) equals 34 pounds per cubic foot (pcf). BUT, the 0.55 relates to dry, in fact, `oven dry’ lumber (dried in an oven so that there’s NO water in it). In `service’, or `real life’, in-place wood will have some water (moisture) in it, and weight more than that determined using the assigned specific gravity. If we look at Page 47 in the 6th edition Timber Construction Manual (TCM), Table 2.2-1, we see a specific weight for SP, at 12% moisture content (another conversation), of 36 pcf. We could use this/that number for how much our rafter weighs. Instead, I’m going to use 50 pcf, since I’m constructing this barn with `green’ lumber.
Here’s the equation …
w = γ A
where
w = the weight per foot of rafter, and
A = cross section area.
Let’s do it …
w = 50 lb per cubic ft x (2 / 12 ft x 6 / 12 ft)
w = 4.17 lb/ft.
Does this make sense? Could a 2 x 6 rafter, green (just cut from the tree), weigh 4 pounds per foot of length?
I would question 0.4 pounds, or 40 pounds … per foot, but maybe 4 is reasonable. Let’s see, … a 12 foot rafter would weigh … 12 x 4 or 48 to 50 pounds? Yeah, maybe.
Let’s calc how much it bends under its own weight.
The formula is …
Δ = 5 w L4 / (384 E I)
where 5 and 384 are just numbers … if you take a course in Mechanics of Materials, and pay attention, you’ll probably prove it …
Δ = deflection at midspan (that’s where it will be sagged the most)
w = weight per length, or `load’, in this case the weight is the load
L = length of the beam (rafter, etc.)
E = Modulus of Elasticity of the wood, and
I = MOI or Moment of Inertia of the wood `section’.
Sometimes (e.g., Page 595 for that same TCM) you’ll see deflection cast in terms of the `Whole’ load, W … W = w L … or …
Δ = 5 W L3 / (384 E I).
This is kind of nice since the `Whole load’ might be easier to get our mind around.
Let’s do it.
The `Whole load’ due to the weight of the rafter is … (at 50 pcf) …
W = w L = 4.17 lb/ft x 12 ft = 50 lb.
E = 1,600,000 psi, from before … (our concentrated load deflection calc), and
I = 36 in.4 …
So,
Δ = 5 W L3 / (384 E I) = 5 (50 lb) (144 in.)3 / (384 x 1,600,000 psi x 36 in.4 )
Δ = I get … 0.036 inches.
Hmmmm.
Gosh, that would be hard to even see! Well, yeah, … when I put that rafter up on the headers, girders, and it’s only carrying itself, I can’t see it sag … so maybe that’s correct?!!!
What if the rafter is carrying the design roof load, of 20 psf? It’s the same equation! But we need to do a bit of crunching first …
w = σ x s
w = 20 psf x 2 ft = 40 lb/ft … hmmm … about 10 times the weight of the rafter itself …
W = 40 x 12 = 480 lb.
Δ = 0.036 in. (40 / 4.2) = 0.34 in.
Seems reasonable. In other words, the sag due to the weigh of the rafter itself is only about a 30th of an inch … but if we load the rafter up to the design roof load (probably a re-roofing project, with workers, shingles, etc.) … the rafter would sag some 1/3rd of an inch.
Let’s look at the deflection due to the whole `light roof’ construction.
w = 5 psf x 2 ft = 10 lb per foot of rafter length
W = w L = 12 ft x 10 lb/ft = 120 lb.
Δ = 5 W L3 / (384 E I) = 5 (120 lb) (144 in.)3 / (384 x 1,600,000 psi x 36 in.4 )
Δ = 0.086 inches … almost 1/10th of an inch.
Still not much. Might be hard to see. The rafter might even warp more than that!
…
Let’s check our work …
Swinging over to … http://www.timbertoolbox.com/Calcs/beamcalc.htm
(Again, I’m not vouching, necessarily, for the content on this site; I don’t know these people … I’m just seeing if they come up with the same thing I do. If they do, I feel comfy with my work. The chances of us both being the same wrong is small. If they don’t come up with what I do, then at least one of us is wrong.)
Gotta do a few calcs first …
Uniform Load … Load on Beam … notice it says `pounds’ … that means we need to use the `Whole’ load … in this case the `Whole’ uniform dead load on the beam (rafter) … W ( = w L) … 120 lb from above.
Span … 12 feet is 144 inches.
Width … 2 in.
Depth … 6 in.
Max allowable fiber stress … we’re not checking fiber stress here, but I’ll just put in, say, 999 (psi)
Modulus of Elasticity … well, to check the above hand calc, I better use the same E … 1,500,000 psi.
Maximum allowable horizontal shear … I’m not checking shear now, but I’ll just put in 180 (psi).
Show Result!
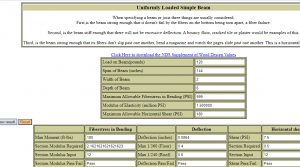
… over to Deflection … 0.0864. Yup; that’s what we got above.
Yay!
…
Oh, let’s talk a bit about … `CREEP’
`Creep’ is long-term deflection.
So, in the example above, I put up the rafter, and it `immediately’ sags a whole 0.036 inches. But if I leave it there, which I will, as time progresses, it will sag (deflect) some more. Let’s say in the mean time I get the rest of the roof up, and, under the (assumed) 5 psf roof dead load, the rafter(s) immediately sags, from above, 0.086 inches. Section 3.5 of the National Design Specification® for Wood Construction (NDS) tells us, essentially, how to handle this.
The long term deflection of a sustained (long-term) load is equal to the short term deflection of that load multiplied by a factor, Kcr. Kcr for seasoned lumber is 1.5; for unseasoned is 2.0. So, since I’m using unseasoned lumber, the long-term deflection of the rafter, carrying the `light’ roof, can be expected to be 2.0 x 0.086 in. = 0.17 in. … somewhere between 1/8th and ¼ of an inch. Maybe I could see it, but no big deal.
If I wait a while, probable at least several months, for this `creep’ thing to take effect … and climb up on the roof (assuming I weight 300 lb – the design concentrated load), and stand on a single rafter, midspan, then the total (midspan) deflection will be the long-term deflection due to the sustained effect of the dead weight of the roof, plus the immediate effect of my weight … from above … 0.17 in. plus 0.35 inches, giving 0.52 inches … about half an inch.
And if I stay up there for a long time (which I won’t!) … the rafter would creep some more, due to the sustained effect of my weight!
JRF